Definition 2.1.2.
A SET is a collection of 3 cards such that for each of the four characteristics, either:
- All three cards share the same value. OR
- All three cards have different values.
Section 2.1 SET
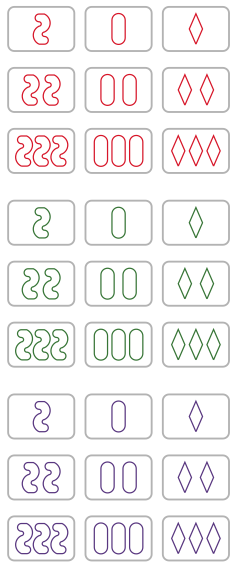
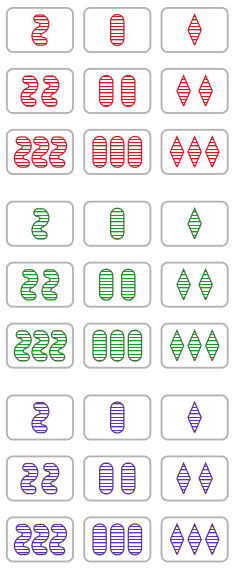
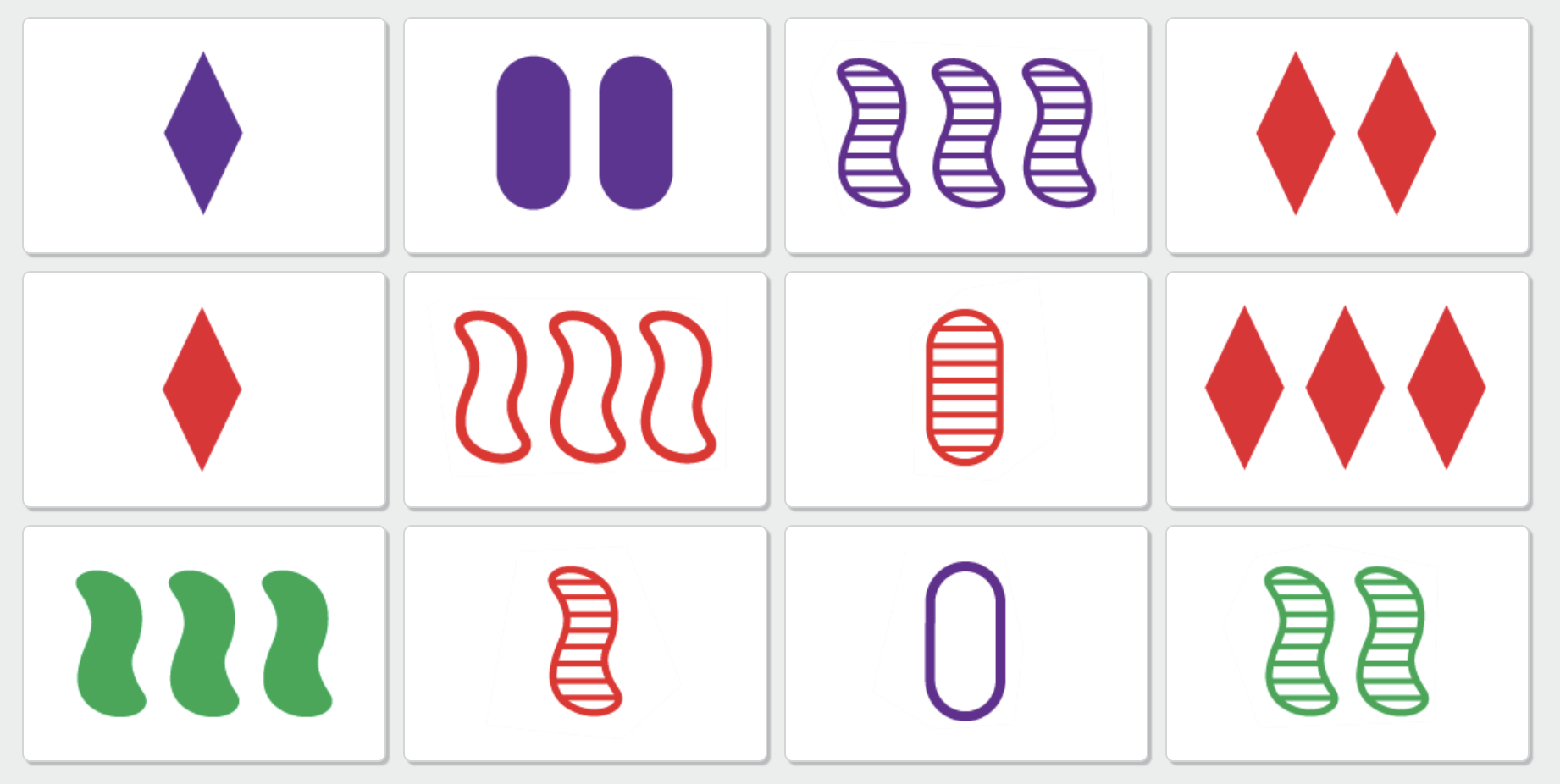
Each SET card has four characteristics.
- Color: Red, Green or Purple.
- Shading: Bold, Empty or Striped.
- Number: One, Two or Three shapes.
- Shape: Oval, Diamonds, or Squiggle.
Activity 2.1.1.
Verify that the following are SETs.
(a)
(b)
(c)
(d)
Activity 2.1.2.
Explain why the following are NOT SETs.
(a)
(b)
(c)
Activity 2.1.3.
(a)
What sets can you find here? 
Figure 2.1.3. 12 SET cards.
(b)
Repeat with the Daily SET Puzzle. 1
Activity 2.1.4.
Play SET!
Activity 2.1.5.
For each of the following, determine what card(s) if any could be added to form a SET:
(a)
(b)
(c)
(d)
Pick any two cards, can you find what card(s) if any will complete a set? Repeat.
Problem 2.1.4.
For any two cards, is it always possible to find a third card to complete a SET? How many options do you have? Justify your assertions.
Activity 2.1.6.
(a)
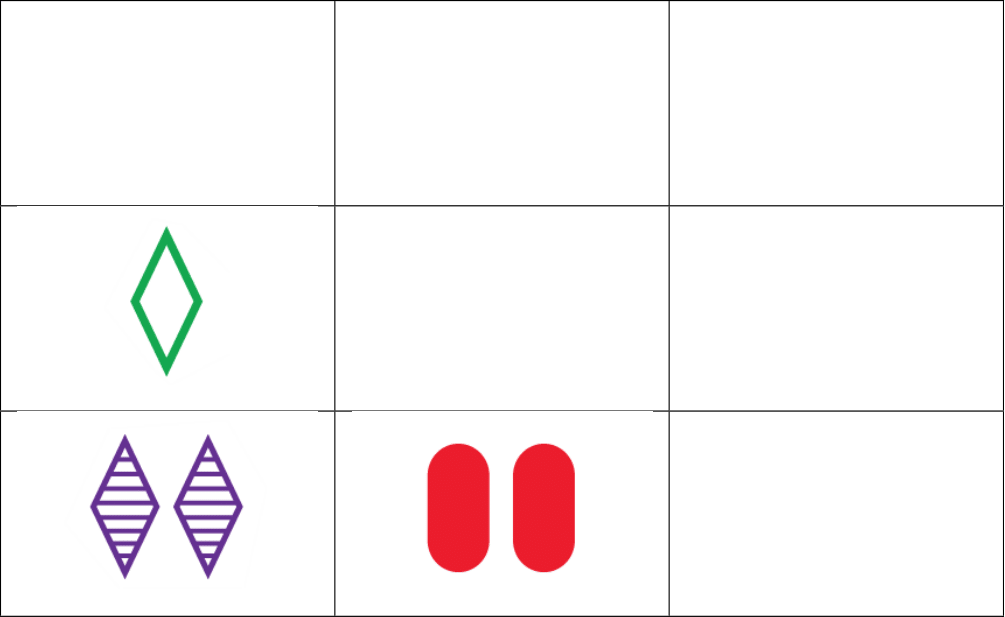
Pick any three cards who do not form a set and arrange them in a corner of a \(3\times 3\) grid like so:
(b)
Fill out this grid so that each row, column and diagonal forms a SET.
(c)
For each pair of cards on this grid, is there a third card also on this grid which forms a SET?
Problem 2.1.5.
For the grid you constructed in Activity 2.1.6, how would you describe the position of the sets in relation to the grid?
